ancient science
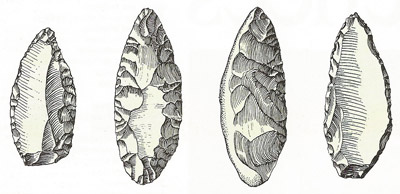
Tools of the middle Paleolithic or Mousterian stage in France date from 70,000 to 32,000 years ago. There were various human groups living in Europe in this period. They left many traces of their culture in shelters and entrances to caves. Tools are found dating from the beginning of the last period of glaciation and the scrapers and knives shown here illustrate fine stone tool technology.
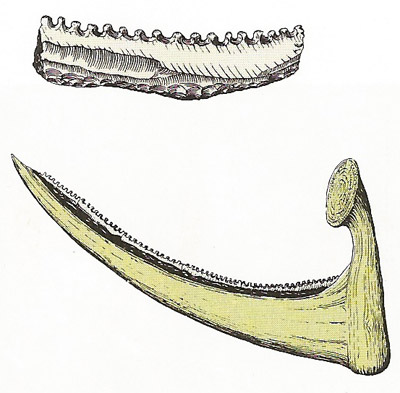
Bones, antlers and wood were used by early man as raw materials for tools and weapons. A wooden tool could be given an efficient cutting edge by adding a row of suitably shaped flint slivers, as in this early Egyptian wooden sickle from about 3000–2500 BC. Pointed wooden implements could also be hardened by charring the point in a fire. Antlers shaped by carving or heating
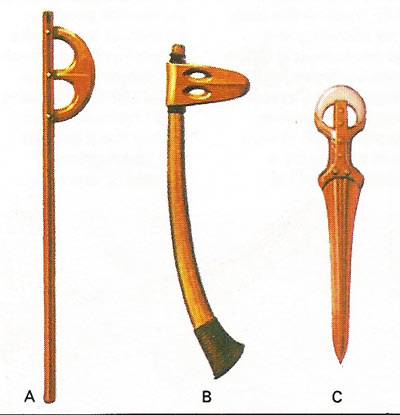
The introduction of metals gave early toolmakers much more manageable raw materials - first soft metals such as gold and copper, later bronze and finally iron. Shown here are an Egyptian eye axe [A] from Megiddo (c. 1900 BC), an Egyptian duck-bill axe [B] from Ugarit (c. 1800 BC) and an Egyptian bronze dagger [C] of the Hyksos period (c. 1650 BC). But iron made the best cutting edge.

The Neolithic people who occupied the region of Stoney Littleton, England in about 3000 BC, constructed large barrows for the burial of their dead. A barrow is a long structure with an entrance passage crossed by transept chambers; this barrow has three pairs. The passage contains a vault with corbels or projections from the walls to carry "capstones", in a manner similar to those in vaults found on islands lying off the coast of Scotland.

The Mesopotamians, lacking the Egyptians papyrus for writing, made records on clay tablets. Characters were formed by pressing the wedge-shaped end of a stylus into the soft clay and a permanent record could be obtained by baking the clay in a fire until it became hard. From its wedge shape, the writing is known as cuneiform. The associated number system used strokes that, to our eyes, faintly resemble the Roman numerals of 30 centuries later. A numeral's position determined its value.
Nearly two million years ago the ancestors of man used stones as weapons and tools. The need to master the environment and develop tools for the purpose involved a primitive knowledge of science. Ever since that time the development of science, technology and civilization have been interrelated.
Science of prehistoric man
After perhaps half a million years, the descendants of these first tool-users, had become more selective, concentrating on flint, with its useful cutting edges. They discovered how to make fires.
Cave paintings of 15,000 years ago indicate a primitive knowledge of animal anatomy. Some, which show prehistoric elephants with the position of the animal's heart indicated by arrows, may be a record of hunting prowess, or a form of sympathetic magic attempting to influence the hunt.
About 10,000 years ago, men began to adopt a more settled way of life. They invented a repetitive system of food production that involved the domestication of animals and the cultivation of plants. Life in such settled communities stimulated invention in various building materials, used to provide better shelter and protection. Fires were kept burning continuously for warmth and cooking and frightening off marauders, and it is possible that the women who tended the fires were the first to notice that when clay is left near a fire it hardens into pottery. When certain stones and earths were roasted in a fire, heavy liquids sometimes ran out which, when cool, hardened into useful metals.
Egypt and Mesopotamia
The people who settled in the Nile valley found themselves in an area that was exceptionally safe and fertile. They noticed that the silt brought down by the yearly floods renewed the fertility of the soil so they dug channels and built embankments to divert the fertile silt-laden flood waters onto their fields. These flood-control operations marked the invention of large-scale engineering. The Nile valley dwellers later applied engineering techniques in the construction of the pyramids.
It is probable that the science of geometry arose from the need to fix positions where landmarks had been washed out by annual flooding. Arithmetic was developed to calculate quantities of crops so that they could be shared among the people. Egyptian arithmetic depended on a method of doubling, much as in the operations of a modern computer. Geometrical surveying led the Egyptians to a good method of calculating the area of a circle; they assumed the circumference of a circle to be a square of eight-ninths times its diameter. They also needed to determine the seasons and the times of the Nile floods and so devised a calendar of 365 days.
The people of Mesopotamia, in the double valley of the rivers Tigris and the Euphrates, were developing in a similar way but under rather different conditions. There was little stone in their land, so they recorded information by making marks on soft clay tablets, which were then baked. The Mesopotamians introduced the idea that the value of a digit depends on its position in a number and they even solved algebraic equations, The Egyptians were primarily concerned with simple, practical calculations whereas the Babylonians were much more sophisticated, especially in connection with the science of astronomy.
One of the first Greeks to visit and study other civilizations was Thales of Miletus, who was born in about 630 BC. He returned from Egypt well versed in the techniques of Egyptian geometry. From experience in building, the Egyptians had learned that if a triangle has two sides of equal length, then the angles at its base are also equal. Thales looked for a way of proving this fact. He made two identical triangles, each with two equal sides, and found that when one was picked up and turned over, it could be laid on top of the other and fitted exactly. In this way, a mathematical proof was developed.
Famous Greek scientists
To Pythagoras, born about 60 years after Thales, is attributed a proof of the famous theorem that the square on the longest side of a right-angled triangle is equal to the sum of the squares on the other two sides. Pythagoras sought to explain the properties of matter in terms of numbers.
Another Greek, Euclid (born 330 BC), provided the basic principles for the teaching of classical geometry that have been used ever since. Less than 50 years later, in 287 BC, Archimedes was born in Sicily. He applied the new mathematics with extraordinary power and logic and made many inventions. He established the principle that, when a body is weighted in a liquid, its apparent loss in weight is equal to the weight of the liquid displaced; he is credited with inventing a screw for raising water from one level to another; and he succeeded in launching a large ship using levers.
Astronomy was first placed on an inadequate scientific basis by Eudoxus, who was born about 408 BC. He showed that the motions of the Sun and planets could be explained by assuming that they moved with uniform motion in perfect circles, the centers of which are near, but not exactly at, the center of the Earth. Later Greek astronomers arranged far more complex systems of circular motions, equalling in accuracy the work of Nicolas Copernicus (1473–1543), nearly 2,000 years later.


