conchoid

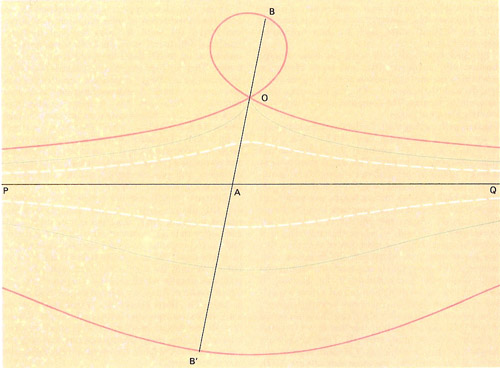
The conchoid of Nicomedes – the three cases:
a = b (blue curve); a > b (white curve); a < b (red curve)

A shell-shaped curve. Given a point A and a curve C, if we pick a point Q on C and draw a line L through A and Q and mark points P and P' on L at some fixed distance in either direction from Q, then the locus of P and P' as Q moves on C is a conchoid.

The conchoid of Nicomedes is a conchoid in which the given line is a straight line; i.e., given a line C and a point A we pick a point Q on C, draw a line L through A and Q, and mark P and P' on L at some fixed distance from Q. The conchoid of Nicomedes is the locus of P and P' as Q moves along C. It has the polar equation r = a sec θ + k.

The conchoid of de Sluze is the curve with the Cartesian equation a(x - a)(x² + y²) = k²x².

Related category

• PLANE CURVES

Also on this site:

Encyclopedia of Alternative Energy & Sustainable Living
Encyclopedia of History

BACK TO TOP