dual
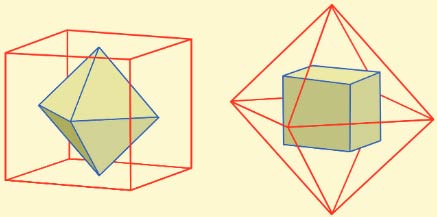
The cube and the octahedron are dual Platonic solids in the sense that the faces and the vertices are interchanged.
The dual of a solid is formed by joining the centers of adjacent faces with straight lines. In the resulting dual solid, each vertex of the dual corresponds to a face on the original, each face on the dual to an original vertex, while the edges match, one for one.
The dual of a tessellation is obtained by replacing each tile with a point at its center, and each edge between tiles with an edge joining vertices. The dual of a regular tessellation is a regular tessellation; the dual of a semi-regular tessellation is not semi-regular.


