flexagon
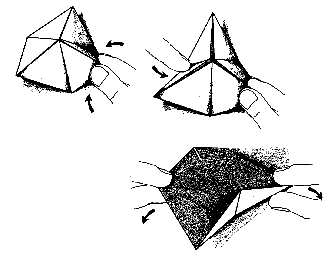
Folding a flexagon.

Hexaflexagons was the subject of the first chapter in Martin Gardner's book, Mathematical Puzzles and Recreations: a collection of Scientific American articles.
A flexagon is a flat model constructed from a folded strip of paper, which, when flexed, can be made to reveal a number of hidden faces. Flexagons are amusing toys but they have also caught the interest of mathematicians. They are usually square or rectangular (tetraflexagons) or hexagonal (hexaflexagons). A prefix can be added to the name to indicate the number of faces that the model can display, including the two faces (back and front) that are visible before flexing. For example, a hexaflexagon with a total of six faces is called a hexahexaflexagon.
The discovery of the first flexagon, a trihexaflexagon, is credited to the British student Arthur H. Stone who was studying at Princeton University in 1939. Stone's colleagues Bryant Tuckermann, Richard P. Feynman, and John W. Tukey became interested in the idea. Tuckerman worked out a topological method, called the Tuckerman traverse, for revealing all the faces of a flexagon. Tukey and Feynman developed a complete mathematical theory that has not been published. Flexagons were introduced to the general public by Martin Gardner writing in Scientific American.1
Reference
1. Gardner, M. Mathematical Puzzles and Diversions. New York: Simon and Schuster, 1959.

