Helmholtz resonator
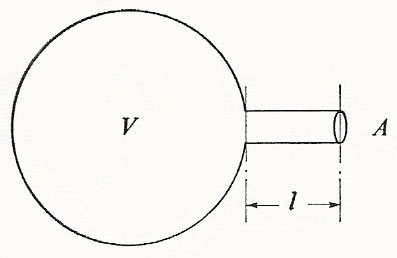
Figure 1. The Helmholtz resonator.
This mechanical system consists of a cavity containing gas connected to the outside by a neck (Figure 1). We set up a simplified model by assuming that the only inertia we have to consider is that of the gas in the neck, which moves backwards and forwards like a piston of mass ρAl, ρ being the density of the gas. When this piston moves as a whole through distance x from its equilibrium position, the change of volume of the air in its cavity is Ax, and the pressure changes may be calculated from the equation of state. Using the adiabatic relation pV γ = constant, we obtain by taking logarithms and differentiating
 |
so that the pressure changes from its equilibrium value by –γpAx/V for a small displacement x of the piston.
Writing the equation of motion for the plug of air
 |
we see that the motion is harmonic with angular frequency


