half-life

Half-life illustrated in a graph of radioactive decay. After the elapse of each half-life period (t½), only half the number (n) of undisintegrated nuclei remain that were present at the beginning of the period. The average time that elapses before a nucleus disintegrates (τ), starting from the beginning of the process (t=0) is given by: τ = 1.443t½.
The half-life is the time taken for a substance or collection of particles to decay by half of its original amount.
Half-life, denoted t½, is a useful concept by which to express the rate of radioactive decay. After one half-life, half of the original number of atoms of a radioactive element will remain. After two half-lives, one-quarter (= ½ × ½) will remain. After three half-lives, 1/8 (= ½ × ½ × ½) will remain, and so on.
The mathematical relationship is exponential and at any time t the number remaining n is given by
n = n0 exp(–λt ),
where n0 is the original number and λ is the decay constant, which is equal to 0.693t½.
The following relationships also exist between the half-life (t½), decay constant (λ), and average lifetime (τ):
t½ = λ–1 · ln 2 = 0.693/λ
λ = t½ · ln 2 = 0.693/t½
τ = 1.443 t½
There are extreme variations in the half-lives of the various radionuclides, e.g. from 7.2 × 1024 years for tellurium-128 down to 2 × 10–16 seconds for beryllium-8.
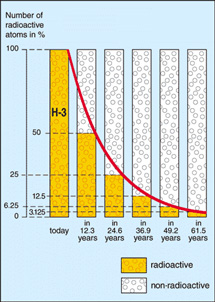 |
| Decay curve of tritium (H-3) –
half-life 12.3 years Credit: European Nuclear Society |


