The Riemann hypothesis is the most important open question in number theory and, possibly, in the whole of mathematics. David Hilbert said: "If I were to awaken after having slept for a thousand years, my first question would be: Has the Riemann hypothesis been proven?" A $1 million prize has been offered by the Clay Mathematics Institute for a proof.

 

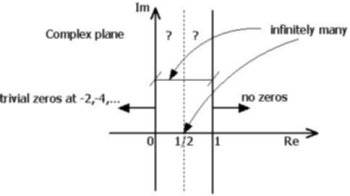
The hypothesis was first formulated by Bernhard Riemann in 1859, was included in David Hilbert's list of challenging problems for twentieth-century mathematicians, and is widely believed to be true. Yet a proof remains tantalizingly out of reach. What the Riemann hypothesis says is that the non-trivial zeros of the Riemann zeta function all have real part equal to 1/2. Broadly speaking, the hypothesis asserts that there is an underlying order, akin to musical harmonics, in the way prime numbers are distributed. It's known that for any given number n there are approximately n/log n prime numbers that are less than n. The formula is not exact: sometimes it is a little high and sometimes a little low. Riemann looked at these deviations and found that they contain periodicities. His hypothesis quantifies and formalizes this discovery, positing that the zeros of the zeta function can be regarded as the harmonic frequencies in the distribution of primes. If the Riemann hypothesis turns out to be true, what do these harmonics in the "music" of the primes mean?

 

Remarkably, it is been found by the English physicist Michael Berry and his colleagues that there is a deep connection between the harmonics – the Riemann zeros – and the allowable energy states of physical systems that are on the border between the quantum world (see quantum mechanics) and the everyday world of classical physics.¹ The Riemann harmonics, or "magic numbers," behave exactly like the energy levels in quantum systems that classically would be chaotic. This deep connection between number theory and the physics of the real universe, if upheld, is utterly astonishing. If the Riemann hypothesis is proved true, it could open an entirely new window on the nature of reality and the relationship between the abstract world of mathematics and the behavior of matter and energy. On the other hand, if it were disproven, there would be an even deeper mystery to explore: How could the Riemann zeta function so convincingly mimic a quantum system without actually being one?

 

Riemann zeta function

We may – paraphrasing the famous sentence of George Orwell – say that "all mathematics is beautiful, yet some is more beautiful than the other." But the most beautiful in all mathematics is the zeta function. There is no doubt about it. —Krzysztof Maslanka, Polish cosmologist

 

The Riemann zeta function is one of the most profound and mysterious objects in modern mathematics. From it has sprung the Riemann hypothesis and all that this conjecture seems to imply. The Riemann zeta function is closely tied to the distribution of prime numbers. It is an extension of the Euler zeta function, first studied by Leonhard Euler, which is the sum

 

 

Euler found that this function is linked to the occurrence of prime numbers by the following fundamental relationship:

 

ζ(s) = 1 + 1/2s + 1/3s + 1/4s + ... = 2n/(2n – 1) × 3n/(3n – 1) × 5n/(5n – 1) × 7n/(7n – 1) × ...

 

The Riemann zeta function extends the definition of Euler's zeta function to all complex numbers. Zeta functions, in general, take the form of infinite sum of negative powers.

 

Reference

1. Berry, Michael. "Quantum Physics on the Edge of Chaos." New Scientist, 116: 44–47 (1987).